Идея линейной регрессии восходит к работам выдающихся математиков и статистиков XIX века:

• Карл Гаусс (1809) — разработал метод наименьших квадратов для предсказания орбиты небесных тел.

• Адриен-Мари Лежандр (1805) — независимо предложил метод наименьших квадратов.

• Фрэнсис Гальтон (1886) — ввел термин "регрессия" при изучении связи между ростом родителей и детей, заметив, что рост детей "регрессирует" к среднему значению.

В XX веке линейная регрессия стала стандартным инструментом в статистике благодаря работам Рональда Фишера и других ученых.

Модели линейной регрессии относительно просты и предоставляют простую для интерпретации математическую формулу, которая может генерировать прогнозы. Линейная регрессия может применяться в различных областях бизнеса и академических исследований.

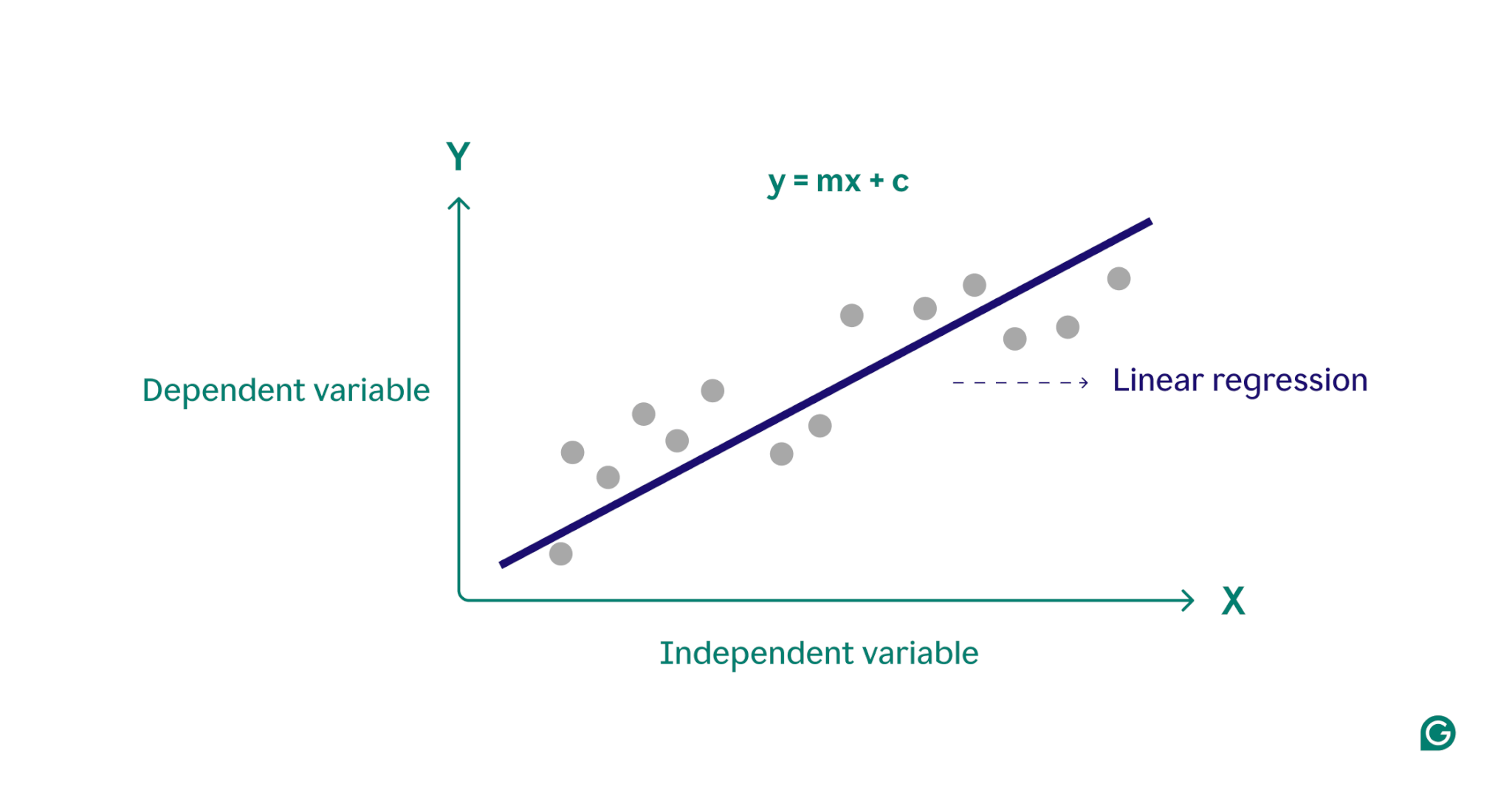Линейная регрессия моделирует зависимость между переменными в виде линейного уравнения:

y=β0+β1x1+β2x2+⋯+βnxn+εy=β0​+β1​x1​+β2​x2​+⋯+βn​xn​+ε

где:

• yy — зависимая переменная (целевое значение),

• x1,x2,…,xnx1​,x2​,…,xn​ — независимые переменные (признаки),

• β0β0​ — свободный член (интерсепт),

• β1,β2,…,βnβ1​,β2​,…,βn​ — коэффициенты регрессии,

• εε — ошибка (шум).

Основные предположения:

1. Линейность связи между переменными.

2. Отсутствие мультиколлинеарности (сильной корреляции между признаками).

3. Нормальное распределение ошибок.

4. Гомоскедастичность (постоянная дисперсия ошибок).

Метод наименьших квадратов (МНК) — стандартный способ нахождения коэффициентов, минимизирующий сумму квадратов ошибок.

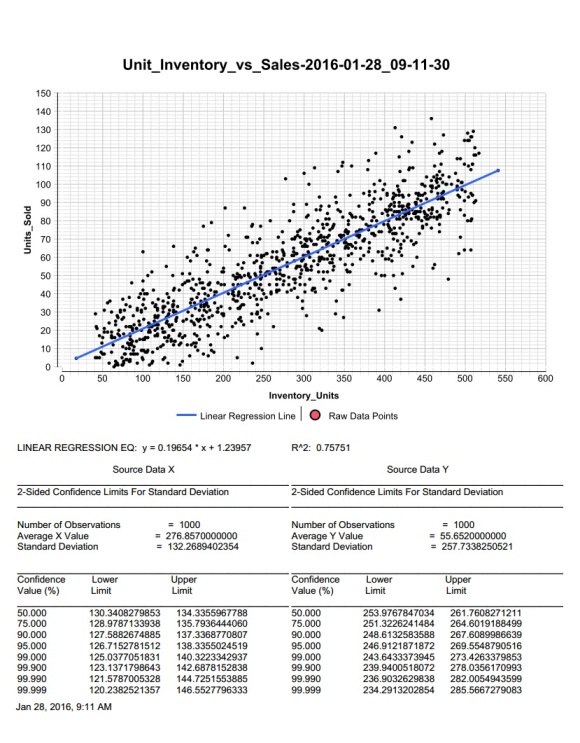Линейная регрессия широко используется в различных областях:

1. Экономика и финансы

   • Прогнозирование цен на акции, спроса на товары.

   • Оценка влияния факторов на ВВП, инфляцию.

2. Маркетинг

   • Анализ эффективности рекламных кампаний.

   • Прогнозирование продаж.

3. Медицина и биология

   • Исследование зависимости уровня заболеваемости от факторов среды.

   • Анализ эффективности лекарств.

4. Техника и производство

   • Оптимизация параметров производственных процессов.

   • Прогнозирование износа оборудования.

5. Машинное обучение

   • Базовый алгоритм для более сложных моделей (ридж-регрессия, лассо).

   • Используется в feature importance-анализе.